58055
14
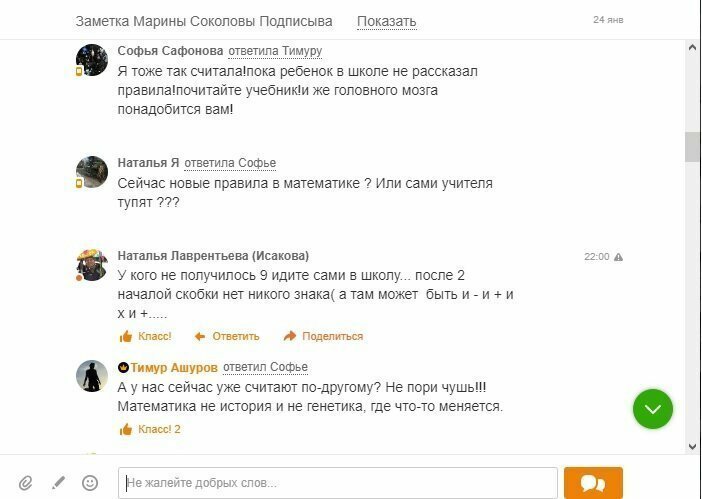
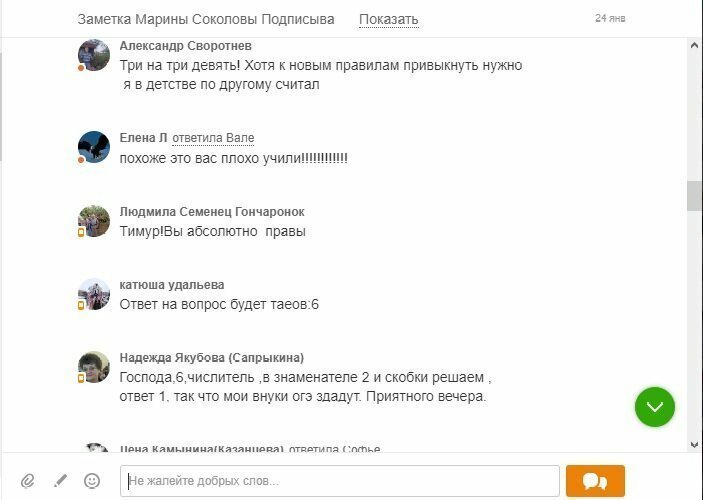
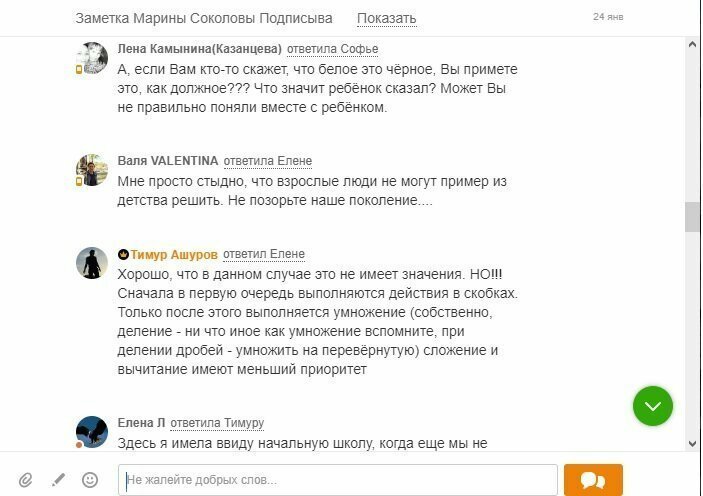
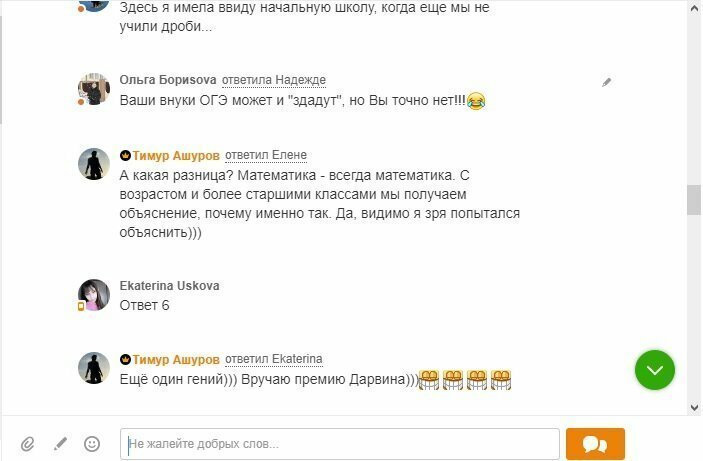
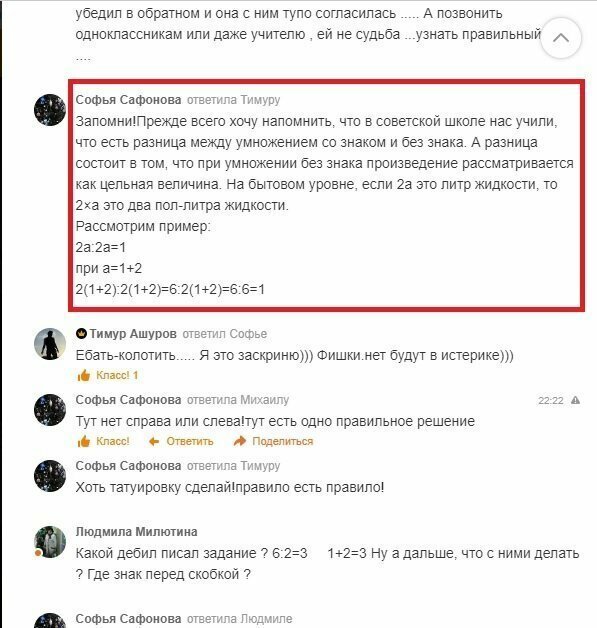
Самое страшное, что люди, получившие образование в СССР, умудряются не просто допускать ошибки, но и нести такую дичь, что становится страшно. Где же мы свернули не туда? Представляю вашему вниманию обсуждение одного примера. Имена не стал замазывать, страна должна знать своих героев.
×
Ссылки по теме:
- Тот случай, когда ты тупой, но не знаешь об этом
- Женщины за 40, которые еще ждут своего принца на белом коне
- Испытание школой: как знаменитые русские поэты и писатели справились с этим
- Творцы из Одноклассников, которые немного слишком увлеклись фотошопом
- Илон Маск удалился из Instagram, но его пригласили «Одноклассники»
Новости партнёров
реклама
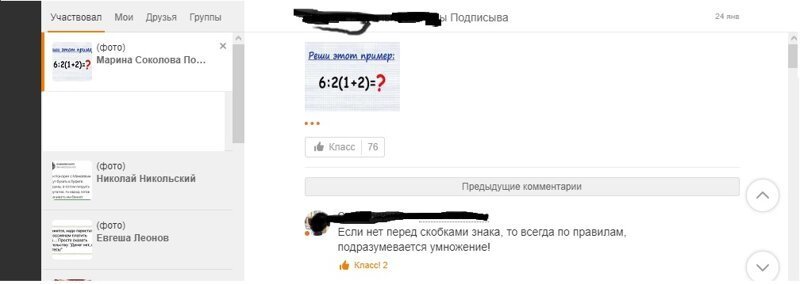
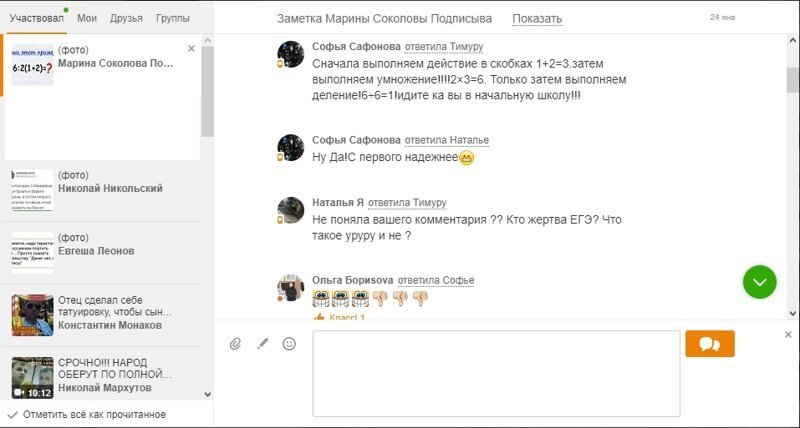
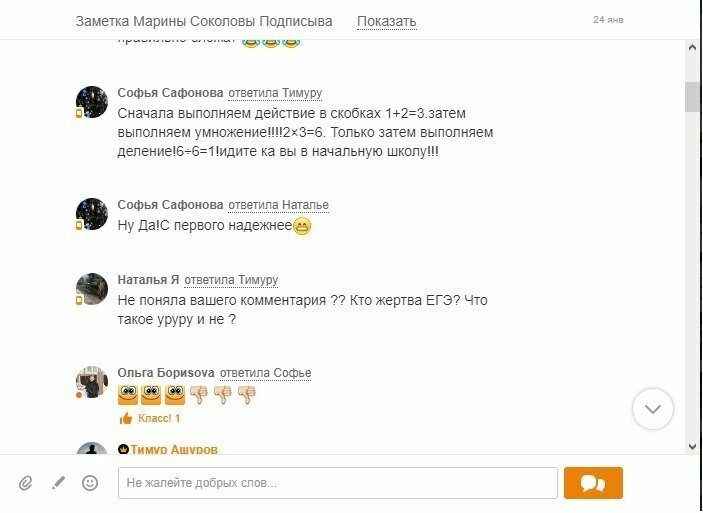
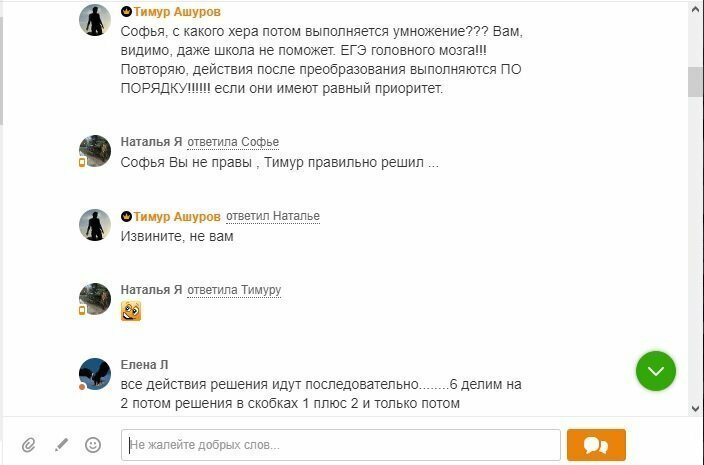
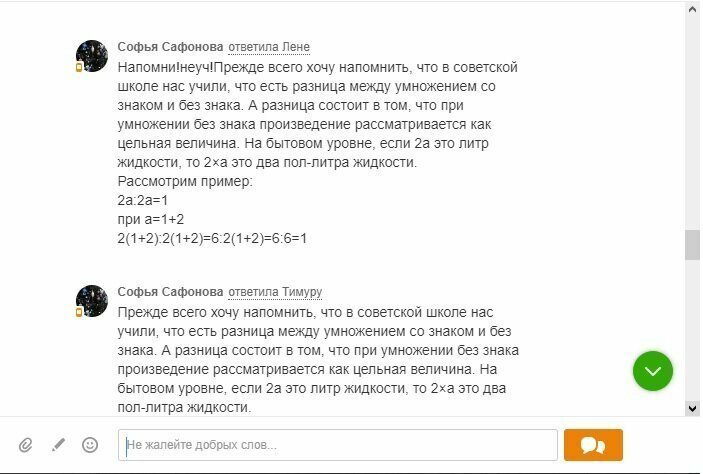
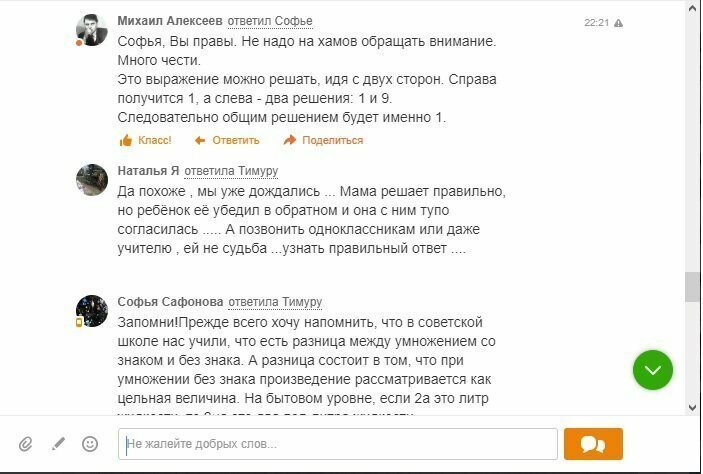
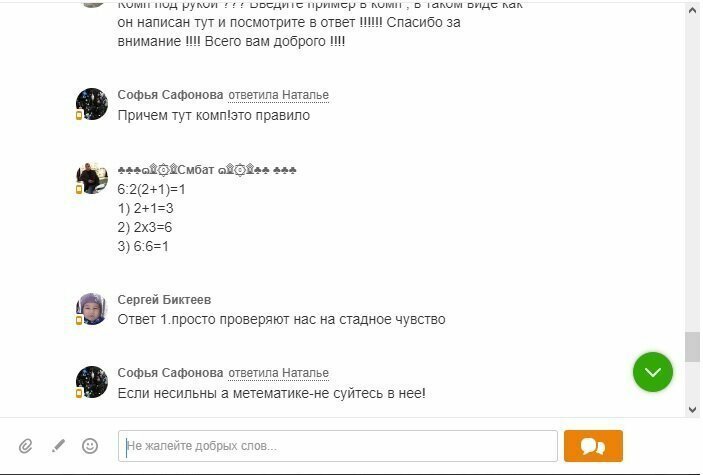
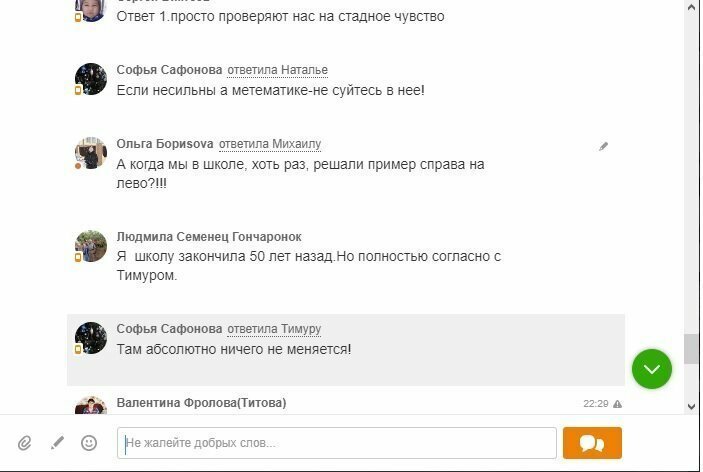
С чего бы знак умножения приоритет вообще поменял?
Это обычная упрощенная форма записи. Деление и умножение всегда были равнозначными (если нет скобок) и вычисляются слева направо.
В школе был отличником по математике и ездил на олимпиады занимая призовые места, получил высшее техническое образование с правом преподавания, сейчас, наверное, седьмой год работаю в школе. Ради интереса даже уточнил и нашего математика по поводу перемены приоритетов в случае отсутствия знака умножения перед скобкой, но подобного бреда ни я, ни наш учитель не слышал еще...
Еще раз учитель подумал и написал мне:
"Изначально задание составлено убого. Знаки в любых официальных источниках ставятся все и всегда и подобное упрощение выражения допускается только по предварительной договоренности.
Но!, даже в случае подобной договоренности, для получения единицы необходимы дополнительные скобки: 62(2+1)). Если скобок нет, то в любом случае будет ответ 9."
"Знак умножения может быть опущен, если ошибка исключена." п.9.5 ГОСТ Р 54521-2011. Кроме того, как раз не требуется никаких договорённостей, это общеупотребимо в математической и технической среде. Это я вам как математик (но не учитель) говорю! ;)
6:2 не может быть множителем, это операция деления двух членов выражения, а не простая дробь. Соответственно, множитель перед скобками - это двойка.
Вы, школьные математики, видимо, привыкли к школьным учебникам, а об институтских книгах и научной литературе давно забыли.
Да и пример тоже явно из высшей математики (еще сарказм))))
Практически никто здесь не смог внятно объяснить как он должен быть решен, и почему именно так, а не иначе.
И, да, математику другую преподают. Не знаю, как в педагогических вузах, а в МИФИ мне было достаточно тяжело изучать высшую математику. До сих пор не могу научиться применять ее на практике, хотя, порой есть необходимость.
Для примера, моя бабушка (учитель математики начальных классов) практически не воспринимает числа больше 1000. Для нее что миллион, что миллиард - одно и то же. А что такое экспоненциальная запись даже знать не хочет. А уж из высшей математики вообще ничего не помнит, хотя, казалось бы, изучала в институте.
А вот родители ежедневно используют высшую математику в своей работе. Так что у меня есть представление об областях знаний знаний математика и учителя математики.
Но это общая проблема - необразованные, непонимающие тему люди рассуждают обо всём на свете, даже не осознавая уровень свой некомпетентности.
Не позорься, просто промолчи, это будет хороший вариант в твоём случае.
Это я к тому, чтобы с тобой случайно по делам не пересечься
шутка)
2(3) - если избегать дополнительных правил "если", введенных в физику и тригонометрию и считать их простыми числами, а не функциями может быть истолковано только как 2*3.
получаем 6:2(1+2) = 6:2*3 = 9
Если вы хотите получить из этого выражения =1, то, по ПРАВИЛАМ алгебры вы должны добавить скобки, а именно:
6: (2(1+2)) = 6: (2(3)) = 6: (2*3) = 6:6 = 1
https://web2.0calc.ru/https://web2.0calc.ru/
Если мы начнем рассуждать на тему что умножение пропуском знака приоритетнее, то мы можем докатится до ситуации в которой 2x3 будет приоритетнее чем 2*3. Ну или наоборот.
На самом же деле, операции умножение и деление - одноранговые операции, выполняющиеся по правилам левой ассоциативности.
И, если буквально интерпретировать правила математики, то значение данного выражения может быть только одно - 9, и никак иначе.
В качестве небольшого подтверждения своих слов приведу скрин, показывающий вычисление данного примера дурой-машиной. Которая следует исключительно правилам математики и которой плевать на субъективное восприятие выражения.
PS
А вообще в реальной математике не принято делать такое записи. В таких случаях как правило рекомендуется использовать горизонтальную дробь, в знаменатель которой загоняется все что нужно, что позволяет избежать всех разночтений.
PPS
Вот вам еще задачка попроще:
1+1*1
только пожалуйста не начинайте тему что : и / это какое то разное деление))
Это я к чему. Напишите математическое правило, согласно которому пропуск знака умножения имеет более высокий приоритет, чем деление?
"это же очевидно" - не доказательство.
"представим другую ситуацию" - тоже не доказательство. У нас тут четкие законы математики, в отличие от американского прецедентного права.
А у тех, кто только арифметику в школе осилил получается «9».
И последних, судя по всему, намного больше.
Ставя мне минус признайтесь, что диплома то у вас нет. А чрезмерная самоуверенность есть.
https://russianclassicalschool.ru/biblio/13_sr_sk_metod_algebra.pdfhttps://russianclassicalschool.ru/biblio/13_sr_sk_metod_algebra.pdf
Знак умножения можно опускать в случаях:
1-Между буквенными множителями
2-Между числовым и буквенным множителем
3-Между множителем и скобкой
4-Между выражениями в скобках
Других вариантов нет. Нельзя опустить знак умножения между двумя числами, например. 1, 2 и 4 варианты нас не интересуют. У нас 3 вариант.
Мое мнение такое, что здесь знак умножения опущен, потому что 2, это множитель вынесенный за скобки. И других вариантов, допускающих опускание знака умножения здесь нет.
https://russianclassicalschool.ru/biblioteka/matematika.htmlhttps://russianclassicalschool.ru/biblioteka/matematika.html
А вот (в рот тебе пароход) из "Методика преподавания алгебры в восьмилетней школе" Репьева В. В.
http://www.mathedu.ru/lib/books/repjev_metodika_prepodavaniya_algebry_1967/#81http://www.mathedu.ru/lib/books/repjev_metodika_prepodavaniya_algebry_1967/#81
a:2(b+c) не равно a:2x(b+c)