53439
5
Вы не раз слышали мнение, что уровень математического образования падает. Во втором классе при закладке самого фундамента математического образования возникает главная проблема - в таблице умножения. Посмотрите на тетради в клетку, которые есть у ваших детей-школьников, на всех - вот такая картина.
Есть тетради еще хуже (для старшеклассников) на которых таблицы умножения нет, а есть куча бессмысленных формул.
Ну, так чем же эта тетрадь плоха? Ничего не подозревающий родитель видит, что на тетради таблица умножения. Вроде, всю жизнь же на тетрадях была таблица умножения? Что не так-то?
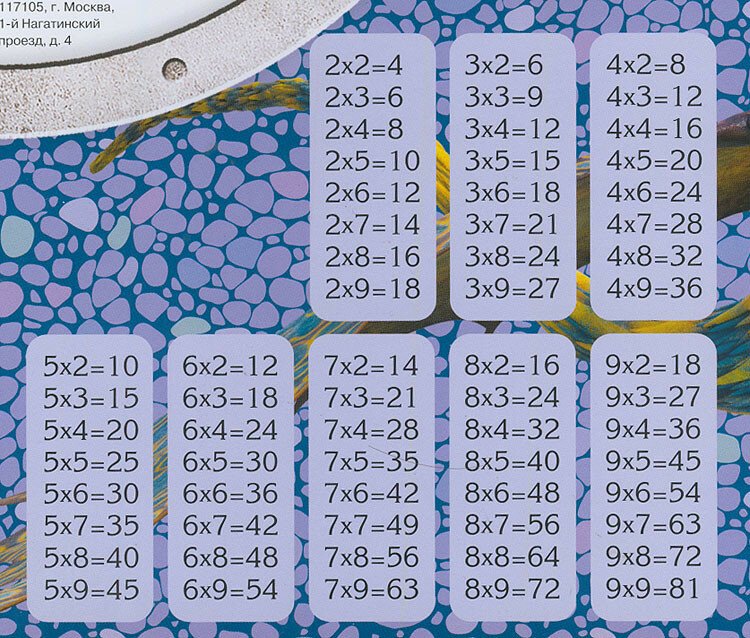
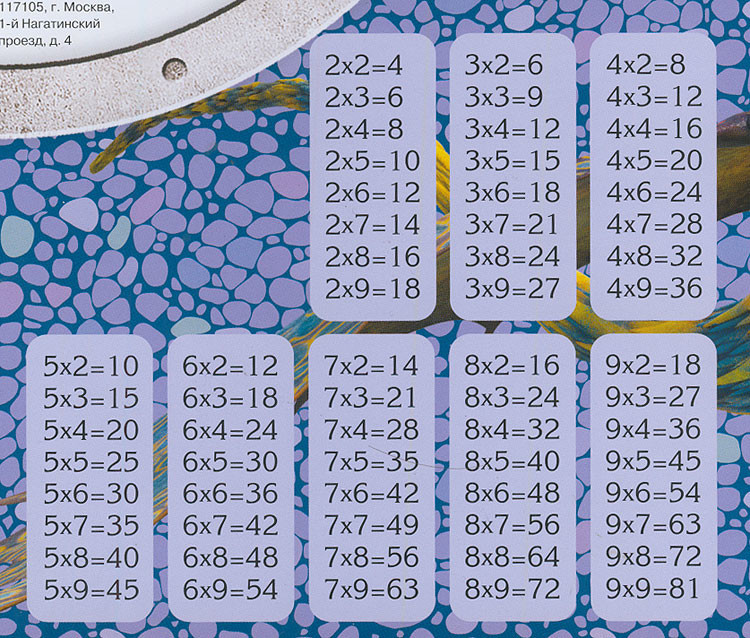
А проблема как раз в том, что на тетради НЕ таблица умножения.
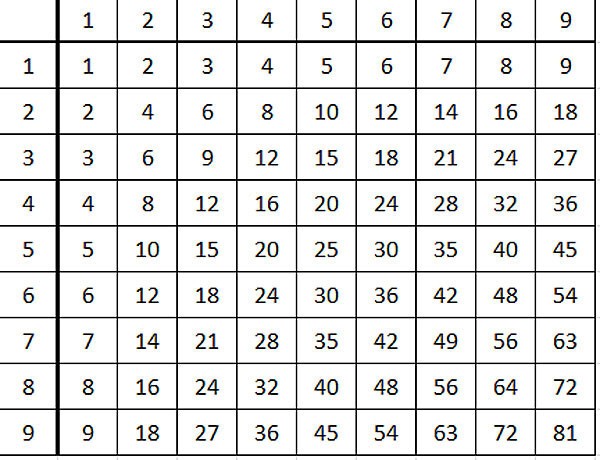
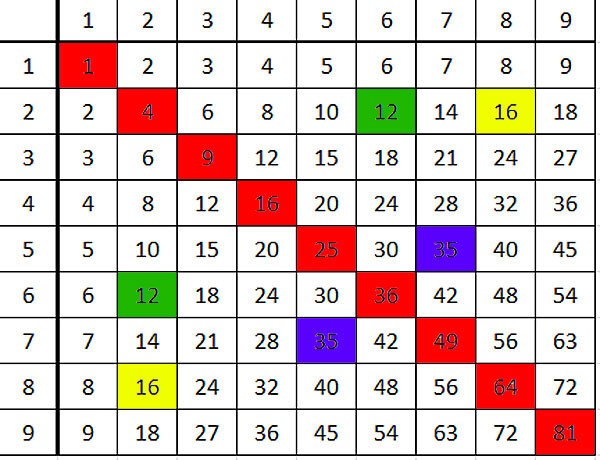
Таблица умножения, дорогие мои читатели, это вот:
Ну, так чем же эта тетрадь плоха? Ничего не подозревающий родитель видит, что на тетради таблица умножения. Вроде, всю жизнь же на тетрадях была таблица умножения? Что не так-то?
А проблема как раз в том, что на тетради НЕ таблица умножения.
Таблица умножения, дорогие мои читатели, это вот:
×
Иногда эту же таблицу даже называют красивым слово "таблица Пифагора". Верхнюю и левую колонки можно не брать, только основной прямоугольник.
Во-первых, это таблица. Во-вторых, она интересная!
Ни один ребенок в здравом уме не будет рассматривать выписанные столбиками примеры.
Ни один ребенок, как бы гениален он ни был, не сможет найти в выписанных примерах интересные фишки и закономерности.
Ну, и вообще, когда учитель говорит: "выучи таблицу умножения", а ребенок даже перед собой таблицы не видит -- он сразу понимает, что математика -- это такая наука, где обычные вещи названы как-то по-другому и надо много-много зубрить, а понять ничего невозможно. И вообще, надо делать "так, как сказано", а не "так, как есть смысл".
Чем же "таблица" лучше?
Во-первых, в ней нет мусора и информационного шума в виде левой части примеров.
Во-вторых, над ней можно подумать. Тут даже нигде не написано, что это умножение -- просто таблица.
В-третьих, если она постоянно под рукой и ребенок на нее постоянно натыкается, он волей-неволей начинает запоминать эти числа. В частности, на вопрос "семью восемь" он никогда не ответит 55 -- ведь числа 55 вообще в таблице нет и не было!
Запоминать столбики примеров способны только дети с аномальной памятью. В "таблице" надо запоминать гораздо меньше.
Кроме того, ребенок автоматом ищет закономерности. И сам самостоятельно их находит. Даже такие закономерности находят дети, еще не умеющие умножать.
Например: числа, симметричные относительно диагонали -- равны. Понимаете, людской мозг просто настроен искать симметрию, и если ее находит и замечает -- очень радуется. А что это означает? Это означает, что от перестановки мест сомножителей произведение не меняется (или что умножение коммутативно, говоря проще).
Во-первых, это таблица. Во-вторых, она интересная!
Ни один ребенок в здравом уме не будет рассматривать выписанные столбиками примеры.
Ни один ребенок, как бы гениален он ни был, не сможет найти в выписанных примерах интересные фишки и закономерности.
Ну, и вообще, когда учитель говорит: "выучи таблицу умножения", а ребенок даже перед собой таблицы не видит -- он сразу понимает, что математика -- это такая наука, где обычные вещи названы как-то по-другому и надо много-много зубрить, а понять ничего невозможно. И вообще, надо делать "так, как сказано", а не "так, как есть смысл".
Чем же "таблица" лучше?
Во-первых, в ней нет мусора и информационного шума в виде левой части примеров.
Во-вторых, над ней можно подумать. Тут даже нигде не написано, что это умножение -- просто таблица.
В-третьих, если она постоянно под рукой и ребенок на нее постоянно натыкается, он волей-неволей начинает запоминать эти числа. В частности, на вопрос "семью восемь" он никогда не ответит 55 -- ведь числа 55 вообще в таблице нет и не было!
Запоминать столбики примеров способны только дети с аномальной памятью. В "таблице" надо запоминать гораздо меньше.
Кроме того, ребенок автоматом ищет закономерности. И сам самостоятельно их находит. Даже такие закономерности находят дети, еще не умеющие умножать.
Например: числа, симметричные относительно диагонали -- равны. Понимаете, людской мозг просто настроен искать симметрию, и если ее находит и замечает -- очень радуется. А что это означает? Это означает, что от перестановки мест сомножителей произведение не меняется (или что умножение коммутативно, говоря проще).
Понимаете, ребенок замечает это сам! А то, что человек придумал сам, он запомнит навсегда, в отличие от того, что он зазубрил или ему сказали.
Помните свой экзамен в вузе по математике? Вы же забыли все теоремы курса, кроме той, что вам досталась, и вам пришлось ее доказывать злобному преподу! Ну, это если вы не списывали, конечно. (Я утрирую, но почти всегда это близко к правде).
А потом ребенок видит, что можно не всю таблицу учить, а только половину. Если мы уже знаем строчку умножения на 3, то нам не надо запоминать "восемь на три", а достаточно вспомнить "три на восемь". Уже вдвое меньше работы.
А кроме того, очень важно, что ваш мозг не принимает сухую информацию в виде каких-то непонятных столбиков примеров, а думает и анализирует. Т.е. тренируется.
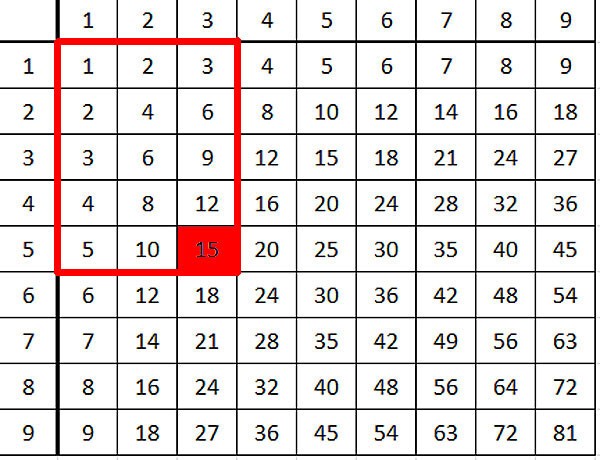
Кроме коммутативности умножения можно заметить, например, еще такой замечательный факт. Если ткнуть в любое число и провести прямоугольник от начала таблицы до этого числа, то количество клеточек в прямоугольнике -- ваше число.
Помните свой экзамен в вузе по математике? Вы же забыли все теоремы курса, кроме той, что вам досталась, и вам пришлось ее доказывать злобному преподу! Ну, это если вы не списывали, конечно. (Я утрирую, но почти всегда это близко к правде).
А потом ребенок видит, что можно не всю таблицу учить, а только половину. Если мы уже знаем строчку умножения на 3, то нам не надо запоминать "восемь на три", а достаточно вспомнить "три на восемь". Уже вдвое меньше работы.
А кроме того, очень важно, что ваш мозг не принимает сухую информацию в виде каких-то непонятных столбиков примеров, а думает и анализирует. Т.е. тренируется.
Кроме коммутативности умножения можно заметить, например, еще такой замечательный факт. Если ткнуть в любое число и провести прямоугольник от начала таблицы до этого числа, то количество клеточек в прямоугольнике -- ваше число.
И тут умножение уже получает более глубинный смысл, чем просто сокращенная запись нескольких одинаковых слагаемых. Идет смысл и для геометрии -- площадь прямоугольника равна произведению его сторон )
А вы не представляете, насколько проще делить с такой таблицей!!!
Короче, если ваш ребенок во втором классе, распечатайте ему вот такую, правильную, таблицу умножения. Повесьте на стену большую, чтобы он на нее поглядывал, когда делает уроки или сидит за компом. Или еще какой дурью страдает. И напечатайте и заламинируйте ему маленькую (или напишите на картоне). Пусть он ее в школу с собой таскает, и просто удобно под рукой держит. (не помешает на такой таблице выделить квадраты по диагонали, чтобы лучше видно)
У моих детей есть -- вот такая. И им это реально помогло во втором классе и до сих пор очень сильно помогает на уроках математики.
А вы не представляете, насколько проще делить с такой таблицей!!!
Короче, если ваш ребенок во втором классе, распечатайте ему вот такую, правильную, таблицу умножения. Повесьте на стену большую, чтобы он на нее поглядывал, когда делает уроки или сидит за компом. Или еще какой дурью страдает. И напечатайте и заламинируйте ему маленькую (или напишите на картоне). Пусть он ее в школу с собой таскает, и просто удобно под рукой держит. (не помешает на такой таблице выделить квадраты по диагонали, чтобы лучше видно)
У моих детей есть -- вот такая. И им это реально помогло во втором классе и до сих пор очень сильно помогает на уроках математики.
Вот, честное слово, сразу средний балл по математике увеличится, а ребенок перестанет ныть, что математика тупая. А в придачу, в будущем вашему ребенку тоже будет проще. Он поймет, что надо шевелить мозгами, а не зубрить. И мало, что поймет, он еще и научится это делать.
И повторюсь: в примерах столбиками ничего плохого нет. И количество информации в них содержится такое же, как и в "таблице". Но и ничего хорошего в таких примерах тоже нет. Это -- информационный мусор, из которого нужное еще не враз найдешь.
И повторюсь: в примерах столбиками ничего плохого нет. И количество информации в них содержится такое же, как и в "таблице". Но и ничего хорошего в таких примерах тоже нет. Это -- информационный мусор, из которого нужное еще не враз найдешь.
Источник:







































































































Во-первых, обе эти таблички были всегда и учили сначала по первой, а потом уже (в более старших классах) объясняли как работать с таблицей Пифагора.
Во-вторых, очень многое зависит от особенностей восприятия конкретного человека - кто-то понимает после подробного объяснения, у другого сразу в мозгу образная картинка рисуется, а третий должен многочисленными повторами каждый раз дополнять картинку новыми штрихами и красками.
Ну и в-третьих все зависит от преподавателя и родителей.
Источник:
А вот и нет. В советское время учили именно таблицу Пифагора. На тетрадях в клеточку на обратной стороне была именно она.
В старших классах таблицу умножения никто уже не учил: к тому времени ее даже двоечники знали.
И даже я помню тетрадки с таблицей умножения (у меня были темно-зеленые, голубые и сиреневые) и как нам по одному столбику говорили выучить начиная от 2 и до 9.
А касательно того, что на тетрадках не было таблицы умножения обратите внимание на год в прикрепленном фото.
У меня, в своё время была сильная обида на математичку, за то, что нам не объясняли как пользоваться таблицей брадиса и логарифмической линейкой. Пришлось познавать самому. Зато, блин, разрешали пользоваться инженерными калькуляторами.
Думаю с увеличением объема этой самой информации нужно увеличивать и продолжительность обучения.
Причем он намеренно или по тупости дает некорректные примеры.
Ведь пять слонов умножить на ноль это взять пять слонов ноль раз - то есть ни разу не взять слонов и получить ноль слонов взятыми.
И так по всем его примерам
Так что, повторюсь. Первая форма - чтобы выучить таблицу. Вторая - чтобы подсмотреть, если забыл. Пользоваться же таблицей Пифагора вместо памяти - это может придумать только "поколение ЕГЭ".