53440
5
Вы не раз слышали мнение, что уровень математического образования падает. Во втором классе при закладке самого фундамента математического образования возникает главная проблема - в таблице умножения. Посмотрите на тетради в клетку, которые есть у ваших детей-школьников, на всех - вот такая картина.
Есть тетради еще хуже (для старшеклассников) на которых таблицы умножения нет, а есть куча бессмысленных формул.
Ну, так чем же эта тетрадь плоха? Ничего не подозревающий родитель видит, что на тетради таблица умножения. Вроде, всю жизнь же на тетрадях была таблица умножения? Что не так-то?
А проблема как раз в том, что на тетради НЕ таблица умножения.
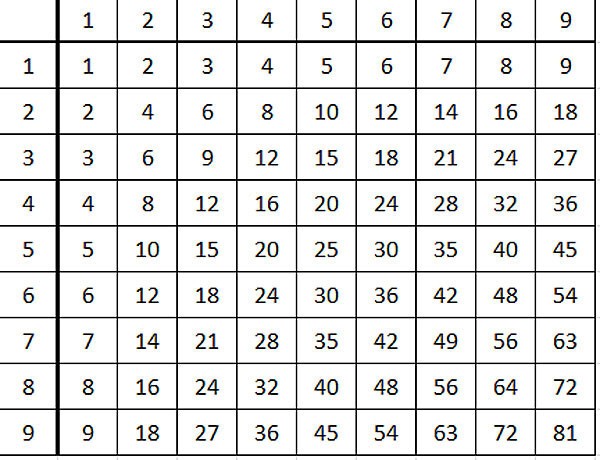
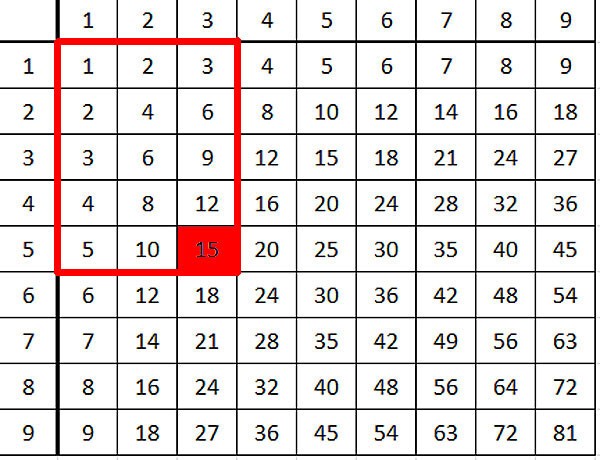
Таблица умножения, дорогие мои читатели, это вот:
Ну, так чем же эта тетрадь плоха? Ничего не подозревающий родитель видит, что на тетради таблица умножения. Вроде, всю жизнь же на тетрадях была таблица умножения? Что не так-то?
А проблема как раз в том, что на тетради НЕ таблица умножения.
Таблица умножения, дорогие мои читатели, это вот:
×
Иногда эту же таблицу даже называют красивым слово "таблица Пифагора". Верхнюю и левую колонки можно не брать, только основной прямоугольник.
Во-первых, это таблица. Во-вторых, она интересная!
Ни один ребенок в здравом уме не будет рассматривать выписанные столбиками примеры.
Ни один ребенок, как бы гениален он ни был, не сможет найти в выписанных примерах интересные фишки и закономерности.
Ну, и вообще, когда учитель говорит: "выучи таблицу умножения", а ребенок даже перед собой таблицы не видит -- он сразу понимает, что математика -- это такая наука, где обычные вещи названы как-то по-другому и надо много-много зубрить, а понять ничего невозможно. И вообще, надо делать "так, как сказано", а не "так, как есть смысл".
Чем же "таблица" лучше?
Во-первых, в ней нет мусора и информационного шума в виде левой части примеров.
Во-вторых, над ней можно подумать. Тут даже нигде не написано, что это умножение -- просто таблица.
В-третьих, если она постоянно под рукой и ребенок на нее постоянно натыкается, он волей-неволей начинает запоминать эти числа. В частности, на вопрос "семью восемь" он никогда не ответит 55 -- ведь числа 55 вообще в таблице нет и не было!
Запоминать столбики примеров способны только дети с аномальной памятью. В "таблице" надо запоминать гораздо меньше.
Кроме того, ребенок автоматом ищет закономерности. И сам самостоятельно их находит. Даже такие закономерности находят дети, еще не умеющие умножать.
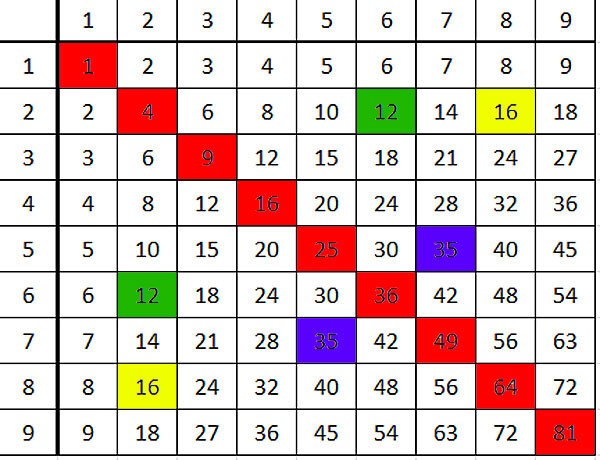
Например: числа, симметричные относительно диагонали -- равны. Понимаете, людской мозг просто настроен искать симметрию, и если ее находит и замечает -- очень радуется. А что это означает? Это означает, что от перестановки мест сомножителей произведение не меняется (или что умножение коммутативно, говоря проще).
Во-первых, это таблица. Во-вторых, она интересная!
Ни один ребенок в здравом уме не будет рассматривать выписанные столбиками примеры.
Ни один ребенок, как бы гениален он ни был, не сможет найти в выписанных примерах интересные фишки и закономерности.
Ну, и вообще, когда учитель говорит: "выучи таблицу умножения", а ребенок даже перед собой таблицы не видит -- он сразу понимает, что математика -- это такая наука, где обычные вещи названы как-то по-другому и надо много-много зубрить, а понять ничего невозможно. И вообще, надо делать "так, как сказано", а не "так, как есть смысл".
Чем же "таблица" лучше?
Во-первых, в ней нет мусора и информационного шума в виде левой части примеров.
Во-вторых, над ней можно подумать. Тут даже нигде не написано, что это умножение -- просто таблица.
В-третьих, если она постоянно под рукой и ребенок на нее постоянно натыкается, он волей-неволей начинает запоминать эти числа. В частности, на вопрос "семью восемь" он никогда не ответит 55 -- ведь числа 55 вообще в таблице нет и не было!
Запоминать столбики примеров способны только дети с аномальной памятью. В "таблице" надо запоминать гораздо меньше.
Кроме того, ребенок автоматом ищет закономерности. И сам самостоятельно их находит. Даже такие закономерности находят дети, еще не умеющие умножать.
Например: числа, симметричные относительно диагонали -- равны. Понимаете, людской мозг просто настроен искать симметрию, и если ее находит и замечает -- очень радуется. А что это означает? Это означает, что от перестановки мест сомножителей произведение не меняется (или что умножение коммутативно, говоря проще).
Понимаете, ребенок замечает это сам! А то, что человек придумал сам, он запомнит навсегда, в отличие от того, что он зазубрил или ему сказали.
Помните свой экзамен в вузе по математике? Вы же забыли все теоремы курса, кроме той, что вам досталась, и вам пришлось ее доказывать злобному преподу! Ну, это если вы не списывали, конечно. (Я утрирую, но почти всегда это близко к правде).
А потом ребенок видит, что можно не всю таблицу учить, а только половину. Если мы уже знаем строчку умножения на 3, то нам не надо запоминать "восемь на три", а достаточно вспомнить "три на восемь". Уже вдвое меньше работы.
А кроме того, очень важно, что ваш мозг не принимает сухую информацию в виде каких-то непонятных столбиков примеров, а думает и анализирует. Т.е. тренируется.
Кроме коммутативности умножения можно заметить, например, еще такой замечательный факт. Если ткнуть в любое число и провести прямоугольник от начала таблицы до этого числа, то количество клеточек в прямоугольнике -- ваше число.
Помните свой экзамен в вузе по математике? Вы же забыли все теоремы курса, кроме той, что вам досталась, и вам пришлось ее доказывать злобному преподу! Ну, это если вы не списывали, конечно. (Я утрирую, но почти всегда это близко к правде).
А потом ребенок видит, что можно не всю таблицу учить, а только половину. Если мы уже знаем строчку умножения на 3, то нам не надо запоминать "восемь на три", а достаточно вспомнить "три на восемь". Уже вдвое меньше работы.
А кроме того, очень важно, что ваш мозг не принимает сухую информацию в виде каких-то непонятных столбиков примеров, а думает и анализирует. Т.е. тренируется.
Кроме коммутативности умножения можно заметить, например, еще такой замечательный факт. Если ткнуть в любое число и провести прямоугольник от начала таблицы до этого числа, то количество клеточек в прямоугольнике -- ваше число.
И тут умножение уже получает более глубинный смысл, чем просто сокращенная запись нескольких одинаковых слагаемых. Идет смысл и для геометрии -- площадь прямоугольника равна произведению его сторон )
А вы не представляете, насколько проще делить с такой таблицей!!!
Короче, если ваш ребенок во втором классе, распечатайте ему вот такую, правильную, таблицу умножения. Повесьте на стену большую, чтобы он на нее поглядывал, когда делает уроки или сидит за компом. Или еще какой дурью страдает. И напечатайте и заламинируйте ему маленькую (или напишите на картоне). Пусть он ее в школу с собой таскает, и просто удобно под рукой держит. (не помешает на такой таблице выделить квадраты по диагонали, чтобы лучше видно)
У моих детей есть -- вот такая. И им это реально помогло во втором классе и до сих пор очень сильно помогает на уроках математики.
А вы не представляете, насколько проще делить с такой таблицей!!!
Короче, если ваш ребенок во втором классе, распечатайте ему вот такую, правильную, таблицу умножения. Повесьте на стену большую, чтобы он на нее поглядывал, когда делает уроки или сидит за компом. Или еще какой дурью страдает. И напечатайте и заламинируйте ему маленькую (или напишите на картоне). Пусть он ее в школу с собой таскает, и просто удобно под рукой держит. (не помешает на такой таблице выделить квадраты по диагонали, чтобы лучше видно)
У моих детей есть -- вот такая. И им это реально помогло во втором классе и до сих пор очень сильно помогает на уроках математики.
Вот, честное слово, сразу средний балл по математике увеличится, а ребенок перестанет ныть, что математика тупая. А в придачу, в будущем вашему ребенку тоже будет проще. Он поймет, что надо шевелить мозгами, а не зубрить. И мало, что поймет, он еще и научится это делать.
И повторюсь: в примерах столбиками ничего плохого нет. И количество информации в них содержится такое же, как и в "таблице". Но и ничего хорошего в таких примерах тоже нет. Это -- информационный мусор, из которого нужное еще не враз найдешь.
И повторюсь: в примерах столбиками ничего плохого нет. И количество информации в них содержится такое же, как и в "таблице". Но и ничего хорошего в таких примерах тоже нет. Это -- информационный мусор, из которого нужное еще не враз найдешь.
Источник:
Еще крутые истории!







































































































Понимание, это конечно хорошо, но таблицу надо прежде всего вызубрить. От ее понимания, ни память не потренируешь, ни саму таблицу не выучишь.
Автору спасибо за отличный пост.
МОЖНО тупо вызубрить. Но тогда для работы в сфере требующей сложных расчётов будет затруднительно - мозг никогда полностью так и не перестроится. Например в проектировании строительных объектов, математическом моделировании в программировании и многих других сферах. Требуется чтобы при любом расчёте не память срабатывала а математическая модель заполненная верными данными.
В прочем продавцам телефонов и работникам макдональдса это лишняя нагрузка на орган использование которого на такой работе требуется как раз минимизировать.
"Автору спасибо за отличный пост."
Для дебилов пост.
Не согласны. Хорошо. Объясните мне, идиоту, как мне поможет, что таблицу умножения я выучил по таблице Пифагора, скажем в программировании?
Не сама таблица а ход мысли. Естественно с возрастом ребёнок перестаёт задумываться решая столь простые задачи но вот от способа которым он получает это явление зависит многое.
- Предположим вы программист и изучаете Адобе флеш. Вы начали изучать версию 4 по русскоязычному учебнику и с трудом но разобрались что к чему, однако ваши навыки никто не будет оплачивать. Во всяком случае нормально. Вы ищете учебник и находите свежий на Русском языке, тратие уйму времени но олучаете навык более- менее востребованные. Но вот платить вам всё равно будут более чем скромно.
Чтобы зарабатывать существенно надо выучить английски язык, читать самые свежие релизы на нём без переводчика, задавать вопросы специалистам в сети - тоже англоязычным ибо из тупо большев данной сфере.
Тот кто изначально владеет английским и начал забираться под руководством грамотных спецов, будет в итоге иметь существенно больше шансов на ХОРОШИЙ доход - скажем 400 000 в Москве в месяц реальный факт из жизни. Причём для рядового програмера.
Тот кто до последнего старался учить по переведённым на Русский учебникам конечно тоже имеет шанс стать профессионалом но значительно меньший из-за не равных стартовых условий. Его пусть будет более "извилист" - изначально не линейным обучением.
-Тоже самое с любым предметом, если материал тупо заучивать то стать ценным специалистом на практике не возможно. Данные имеют ошиби, исключения, применяются не всегда так как написано в учебниках и не очевидным образом. То что отличает специалиста вовсе не масса накопленных фактов, а умение ими пользоваться - а для этого желательно изначально не зубрить а запоминать на базе закономерностей и понимания.
- В идеале, советская система строилась именно орентируясь на данный принцип, естественно результат был долёк о идеалы но наше образование до 80 года котируется почти везде. Во многих странах диплом даже подтверждать не надо - а вот свежий дипломчик в тех же штатах можете смело выкинуть на помойку- в перечне всего пара Российских институтов чьи корочки вообще можно подтвердить. Дегродация-с.
И пример с нафиг никому не нужным флэшем - очень показательный.
Я то работаю руками )
Так что привожу примеры которые знаю.
Мог бы ещё про маму - инженера проектировщика рассказать но это простыня на километр выйдет. Кто в курсе как без автокада проектируются здания тот со мной согласится - а кто телефонами торгует - хоть об объясняйся не поймёт.
-В прочем проектировщиков - зубрил тоже хватает. Когда на стройку приходят проекты после проверки а там лесничные парши в воздухе висят или в дверные проёмы по проекту входят. Куча аких вот зубрил работает и не видят ошибки в своих расчётах ибо тупо запомнили как считать и чтобы найти ошибку надо им снова просчитать с нуля, а тем кто понимает что считает и почему именно так видят ошибки в расчётах визуально. Как в примере самой статьи - ну нет в таблице умножения такой цифры ! И пересчитывать не надо, когда тупо запомнив надо пересчитывать или вспоминать.
Память - это не запись в книге или таблице. Она работает иначе.
Есть принципиальная разница запомнить тупо набор решений или запомнить решения исходя из принципа данные решения сформировавшие. Память ассоциативная на порядок эффективнее.
- С буквами всё НАМНОГО сложнее. Этим целые НИИ занимаются. Ваш вопрос был бы корректен к носителю языка где письменность иероглифическая. Там есть выбор - запоминать принцип формирования символа ( как учат японцев к примеру ) или тупое запоминание ( которое с тем же Японским языком почти не возможно из-за чудовищного объёма запоминания. Там отдельные элементы и символы могут образовывать новые иероглифы и учить все за пределами возможностей большинства людей просто физически )
Русский же язык зубрят скорее из-за отсутствия нормальной системы образования.
Была такая вещь когда то. АзБуКа. Не та что у каждой буквы говнокартинка а классическая.
к сожалению вернутся к старославянской системе не выйдет - конечно безграмотное письмо при той системе образования было почти не возможно. Ошибиться в написании слова было сложнее чем сейчас перепутать сигнал на светофоре. Но со временем язык впитал в себя гигантское число иностранных слов вместо формирования собственных и было привнесено чудовищное количество искажений и исключений не подчиняющихся правилам самого языка.
Но учил я именно по первому. И никогда не занимался анализом таблицы Пифагора.
Интересно, на чем основаны выводы автора? На его личном суждении?
В 40-х годах (сразу после войны!) полноценно усваивали все разделы математики 80% школьников, учившихся "по Кисёлеву"
Учебники Киселёва Андрея Петровича ( Арифметика , Алгебра , Геометрия )
https://cloud.mail.ru/public/3VpSH9ToDTdN/KISELEV.ziphttps://cloud.mail.ru/public/3VpSH9ToDTdN/KISELEV.zip
Какой тендер?
А вот примеры с несколькими преобразованиями решать в уме = это здорово. Но в этом случае, если ученик допустил где то ошибку, преподаватель не имеет возможности его поправить, т.к. не понятно где он её допустил.
А вот великий педагогический талант некоторых учителей для моего скудного разума непостижим.