69046
2
Австралийским старшеклассникам во время общегосударственного тестирования подкинули задачку по геометрии, поставившую большую часть школьников в тупик. В социальных сетях поднялась буча: мол, какого хрена такие мозголомные задания вносить в экзамен.
Условие:
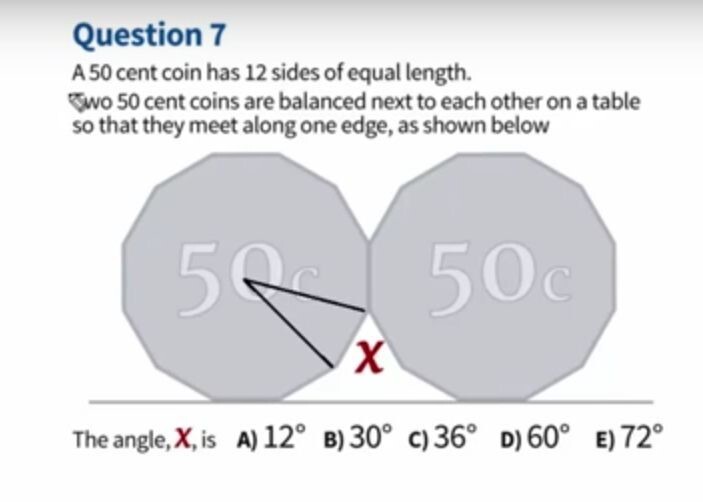
Монета в 50 центов имеет 12 граней одинаковой длины.
Две монеты поставили вплотную друг к другу на столе так, как показано на картинке.
Нужно найти угол X. Тот, который между двумя монетами.
Монета в 50 центов имеет 12 граней одинаковой длины.
Две монеты поставили вплотную друг к другу на столе так, как показано на картинке.
Нужно найти угол X. Тот, который между двумя монетами.
Дальше читайте после самостоятельного решения.....Я показал эту задачу дочке студентке - она пощелкала айфоном и выдала мне ровно половину правильного ответа (потому что спешит).
У меня нет высшего образования. Но я решил эту задачу за 15 секунд в голове.
Правильный ответ - (сто восемьдесят разделить на три)
Хронология моего решения - 360 делим на 12 а так как монет две то умножаем на 2.
P.S. В самом начале (еще до решения) Беглым взглядом посмотрел на угол X мозг сразу выдал градусов шестьдесят примерно...Как говорится глаз алмаз...
У меня нет высшего образования. Но я решил эту задачу за 15 секунд в голове.
Правильный ответ - (сто восемьдесят разделить на три)
Хронология моего решения - 360 делим на 12 а так как монет две то умножаем на 2.
P.S. В самом начале (еще до решения) Беглым взглядом посмотрел на угол X мозг сразу выдал градусов шестьдесят примерно...Как говорится глаз алмаз...
Ссылки по теме:
- Чем же запомнился 2016 год?
- Основные тренды зимней моды, которые просто не укладываются в голове
- "Не трогай! Это на новый год!" - эта фраза вновь актуальна
- Первый Новый год без родителей: бесконтрольное веселье и печальный итог
- Встречу Новый Год наедине с президентом: о тех, кто отмечает праздник в одиночестве



































































































Автор накосячил с рисунком!
Сумма внешних углов многоугольника, взятых по одному при каждой его вершине, равна 360^.
Доказательство:
Каждый внешний угол многоугольника вместе со смежным внутренним составляет 180^ (например, углы при вершине E). Таких пар углов будет n, поэтому сумма всех внутренних углов и внешних (взятых по одному при каждой вершине) составляет 180^ n. Вычтя из нее сумму внутренних углов, получим искомую сумму внешних углов: 180^ n-180^ (n-2) = 180^ n - 180^ n + 360^ = 360^ (она не зависит от числа сторон n).
ЗЫ: ^ - это градус)
На самом деле решений множество. И все они простые и быстрые.
Russo Turisto же предлагает определить углы исходя из того, что треугольник равносторонний. Это неверный подход. Доказать, что получившийся треугольник равносторонний другим способом (без определения равенства его углов) довольно трудно.
360/12*2=60
Вспомните как по-моему Нильс Бор на экзамене определял высоту башни или здания. Очевидно, что задачу можно решить многими способами, но тут даны 12ти гранники. Дали бы другие фигуры, решали бы по-другому.
Но в таком случае ничего не мешало вам сразу предположить, что угол равен 60. И угадать (или не угадать). Можно ли такой подход считать решением? Однозначно, нет.
Тк грани равны, то они образуют равносторонний треугольник.
180/3 = 60.