22848
11
Ученые и философы с давних времен развлекали себя внутренне противоречивыми утверждениями, которые крайне сложно объяснить.
Дихотомия Зенона
Чтобы преодолеть путь, нужно сначала преодолеть половину пути. А чтобы преодолеть половину пути, нужно сначала преодолеть половину половины, и так до бесконечности. Поэтому движение никогда не начнется.
Древнегреческий философ Зенон Элейский так доказывал, что утверждение о непрерывности и неограниченной делимости времени и пространства имеет логические трудности.
Древнегреческий философ Зенон Элейский так доказывал, что утверждение о непрерывности и неограниченной делимости времени и пространства имеет логические трудности.
Стрела Зенона
Летящая стрела неподвижна, так как в каждый момент времени она занимает равное себе положение, то есть покоится. Поскольку она покоится в каждый момент времени, то она покоится во все моменты времени, то есть не существует момента времени, в котором стрела совершает движение.
Это еще одна апория Зенона Элейского, в которой он отрицал мыслимость движения. С этого парадокса началась долгая дискуссия о природе времени, которая не завершилась до наших дней.
Это еще одна апория Зенона Элейского, в которой он отрицал мыслимость движения. С этого парадокса началась долгая дискуссия о природе времени, которая не завершилась до наших дней.
×
Корабль Тесея
Если все составные части исходного объекта были заменены, остается ли объект тем же объектом?
Этот парадокс описал Плутарх — древнегреческий писатель и философ. Корабль, на котором Тесей вернулся с Крита в Афины, хранили несколько сотен лет и каждый год отправляли со священным посольством на Делос. При починке в нем постепенно заменяли доски, пока среди философов не возник спор, тот ли это еще корабль, или уже другой, новый?
Этот парадокс описал Плутарх — древнегреческий писатель и философ. Корабль, на котором Тесей вернулся с Крита в Афины, хранили несколько сотен лет и каждый год отправляли со священным посольством на Делос. При починке в нем постепенно заменяли доски, пока среди философов не возник спор, тот ли это еще корабль, или уже другой, новый?
Парадокс всемогущества
Сможет ли всемогущее существо создать камень, который не сможет поднять?
Если да — то оно не сможет поднять камень и перестанет быть всемогущим. Если нет — значит, оно и не было всемогущим. Иногда этот парадокс используют как доказательство невозможности существования Бога, однако богословы утверждают, что представление о беспредельном всемогуществе, пренебрегающем законами логики, чуждо ортодоксальному христианству.
Если да — то оно не сможет поднять камень и перестанет быть всемогущим. Если нет — значит, оно и не было всемогущим. Иногда этот парадокс используют как доказательство невозможности существования Бога, однако богословы утверждают, что представление о беспредельном всемогуществе, пренебрегающем законами логики, чуждо ортодоксальному христианству.
Парадокс Греллинга — Нельсона
Представьте, что в языке появилось два новых класса — автологичные и гетерологичные прилагательные. Каждое прилагательное принадлежит к одному из этих классов. Автологичные — это прилагательные, которые описывают себя. Например, прилагательное «русское» — русское, «многосложное» — многосложное, а «пятисложное» — пятисложное.
Гетерологичные прилагательные себя не описывают. Например, «новое» не является новым, «горячее» — горячим, а «английское» — английским.
Вопрос: к какой из двух групп относится само прилагательное «гетерологичный»? Если оно автологичное, то должно обладать обозначаемым свойством и быть гетерологичным. Если же оно гетерологичное, то свойства из названия у него быть не должно — значит, оно не может быть гетерологичным.
Гетерологичные прилагательные себя не описывают. Например, «новое» не является новым, «горячее» — горячим, а «английское» — английским.
Вопрос: к какой из двух групп относится само прилагательное «гетерологичный»? Если оно автологичное, то должно обладать обозначаемым свойством и быть гетерологичным. Если же оно гетерологичное, то свойства из названия у него быть не должно — значит, оно не может быть гетерологичным.
«Уловка-22»
Человек, который является сумасшедшим, может быть освобожден от выполнения боевого долга по его просьбе. Однако всякий, кто пытается уклониться от выполнения боевого долга, не является подлинно сумасшедшим.
Парадокс, который стал названием одноименных книги и фильма, оказался хорошим примером внутренне противоречивых ситуаций — в том числе и на воинской службе.
Парадокс, который стал названием одноименных книги и фильма, оказался хорошим примером внутренне противоречивых ситуаций — в том числе и на воинской службе.
Парадокс интересных чисел
1 — первое ненулевое натуральное число, 2 — наименьшее простое число, 3 — первое нечетное простое число, 4 — наименьшее составное число… Если попытаться разделить все натуральные числа на «интересные» и «неинтересные», окажется, что все натуральные числа — интересные. Ведь если существует непустое множество неинтересных натуральных чисел, то в этом множестве есть наименьшее число. А наименьшее неинтересное число уже само по себе интересно — и это создает противоречие.
Парадокс пьяницы
Парадокс из области формальной логики утверждает, что в любом баре существует по крайней мере один такой человек, для которого верно, что если он пьет, то пьют все.
Допустим, в баре пьют все. Тогда для любого посетителя верно утверждение, что если пьет он, то пьют и все. Если же неверно, что в кабаке пьют все, тогда в кабаке существует по крайней мере один человек, который не пьет. Поскольку неверно, что он пьет, то верно, что если он пьет, то пьют все.
Допустим, в баре пьют все. Тогда для любого посетителя верно утверждение, что если пьет он, то пьют и все. Если же неверно, что в кабаке пьют все, тогда в кабаке существует по крайней мере один человек, который не пьет. Поскольку неверно, что он пьет, то верно, что если он пьет, то пьют все.
Парадокс дней рождения
В группе, состоящей из 23 или более человек, вероятность совпадения дней рождения (число и месяц) хотя бы у двух людей превышает 50%. То есть более вероятно, что у каких-то двоих дни рождения совпадут, чем то, что у каждого будет своя неповторимая дата.
Интуитивно может показаться, что шансы на совпадение дней рождения крайне низкие. Однако нужно учитывать, что речь идет про вероятность совпадения дней рождения у любых двух человек в группе. Эта вероятность определяется количеством пар людей, которые можно составить из 23 человек. Общее число таких пар равно числу сочетаний из 23 по 2, то есть (23×22) / 2 = 253 пары.
Если в комнате только два человека, то шанс, что их дни рождения совпадают, — 1/365 (для невисокосных лет), а шанс, что не совпадают, — 364/365. Для группы из трех человек вероятность того, что все дни рождения разные считается так: 364/365×363/365. Чем больше группа, тем меньше шанс на уникальность каждого, для группы из 23 человек, вероятность станет ниже 50%.
Интуитивно может показаться, что шансы на совпадение дней рождения крайне низкие. Однако нужно учитывать, что речь идет про вероятность совпадения дней рождения у любых двух человек в группе. Эта вероятность определяется количеством пар людей, которые можно составить из 23 человек. Общее число таких пар равно числу сочетаний из 23 по 2, то есть (23×22) / 2 = 253 пары.
Если в комнате только два человека, то шанс, что их дни рождения совпадают, — 1/365 (для невисокосных лет), а шанс, что не совпадают, — 364/365. Для группы из трех человек вероятность того, что все дни рождения разные считается так: 364/365×363/365. Чем больше группа, тем меньше шанс на уникальность каждого, для группы из 23 человек, вероятность станет ниже 50%.
Парадокс дружбы
У большинства людей друзей меньше, чем в среднем у их друзей.
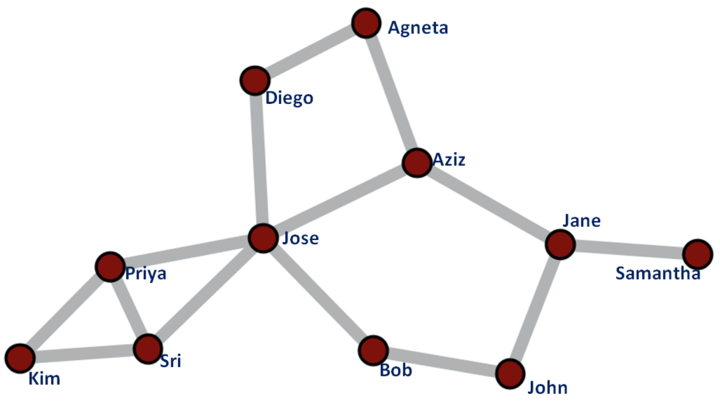
Несмотря на видимую парадоксальность утверждения, оно вполне математически логично и выводится из базовых принципов теории графов. В 2012 году это утверждение подтвердили исследователями Корнеллского университета, которые проанализировали 721 миллион пользователей Facebook*
Несмотря на видимую парадоксальность утверждения, оно вполне математически логично и выводится из базовых принципов теории графов. В 2012 году это утверждение подтвердили исследователями Корнеллского университета, которые проанализировали 721 миллион пользователей Facebook*
Причинно-следственная петля
Физика, работающего над изобретением машины времени, посещает старшая версия его самого и отдает ему чертежи машины времени. Младшая версия использует эти планы для создания машины времени, а после становится старше и возвращается в прошлое, чтобы передать чертежи самому себе.
Путешествия во времени, если они возможны, таят в себе немало парадоксов. Эта ситуация не дает ответа на вопрос: откуда взялись чертежи?
Путешествия во времени, если они возможны, таят в себе немало парадоксов. Эта ситуация не дает ответа на вопрос: откуда взялись чертежи?
* Запрещены в РФ


























































































Обратное так же верно: любой мальчик при дуре - придурок.
придурок=полудурок..
-Мы работаем над кислотой которая сможет растворить любое вещество!
- А в чем Вы будете её хранить?
вопрос о стреле - это вопрос о дискретности пространства и времени
вопрос этот не решен до конца
в школе может казаться что переход к бесконечно малым величинам и пределам все решает,
но это не так
Вопрос состоит вот в чем: стрела движется непрерывно ("проходя через каждую точку") или дискретно ("прыгая" из одной точки в другую на определенном расстоянии от первой)?
до сих пор ответа нет на этот вопрос (скорее всего, нужно отказаться от канторовского точечного континуума, но как - пока нет хороших идей)
подробнее можно почитать тут: https://ru.wikipedia.org/wiki/Апории_Зенона#Современная_трактовкаhttps://ru.wikipedia.org/wiki/Апории_Зенона#Современная_трактовка
"Серьёзные исследования апорий Зенона рассматривают физическую и математическую модели совместно. Р. Курант и Г. Роббинс полагают, что для разрешения парадоксов необходимо существенно углубить наше понимание физического движения[33]. С течением времени движущееся тело последовательно проходит все точки своей траектории, однако если для любого ненулевого интервала пространства и времени нетрудно указать следующий за ним интервал, то для точки (или момента) невозможно указать следующую за ней точку, и это нарушает последовательность. Остаётся неизбежное расхождение между интуитивной идеей и точным математическим языком, предназначенным для того, чтобы описывать её основные линии в научных, логических терминах. Парадоксы Зенона ярко обнаруживают это несоответствие.
Гильберт и Бернайс высказывают мнение, что суть парадоксов состоит в неадекватности непрерывной, бесконечно делимой математической модели, с одной стороны, и физически дискретной материи, с другой[34]: мы вовсе не обязательно должны верить в то, что математическое пространственно-временное представление движения имеет физическое значение для произвольно малых интервалов пространства и времени . Другими словами, парадоксы возникают из-за некорректного применения к реальности идеализированных понятий точка пространства и момент времени , которые не имеют в реальности никаких аналогов, потому что любой физический объект имеет ненулевые размеры, ненулевую длительность и не может быть делим бесконечно.
Близкие точки зрения можно найти у Анри Бергсона и у Николя Бурбаки. Согласно Анри Бергсону[35]:
Противоречия, на которые указывает школа элеатов, касаются не столько самого движения как такового, сколько того искусственного преобразования движения, которое совершает наш разум.
Бергсон полагал, что есть принципиальная разница между движением и пройденным расстоянием. Пройденное расстояние можно произвольно делить, между тем как движение произвольному делению не поддаётся. Каждый шаг Ахиллеса и каждый шаг черепахи должны рассматриваться как неделимые. Это же относится и к полёту стрелы:
Истина заключается в том, что если стрела выходит из точки А и попадает в точку В, то её движение АВ так же просто, так же неразложимо поскольку это есть движение, как напряжение пускающего её лука.
Бергсон А. Творческая эволюция. Глава четвёртая. Кинематографический механизм мышления и механистическая иллюзия. Взгляд на историю систем, реальное становление и ложный эволюционизм
Согласно Николя Бурбаки[36]:
Вопрос о бесконечной делимости пространства (бесспорно, поставленный ещё ранними пифагорейцами) привёл, как известно, к значительным затруднениям в философии: от Элеатов до Больцано и Кантора математики и философы не в силах были разрешить парадокса как конечная величина может состоять из бесконечного числа точек, не имеющих размера.
Замечание Бурбаки означает, что необходимо объяснить: каким образом физический процесс за конечное время принимает бесконечно много различных состояний. Одно из возможных объяснений: пространство-время в действительности является дискретным, то есть существуют минимальные порции (кванты) как пространства, так и времени[37]. Если это так, то все парадоксы бесконечности в апориях исчезают. Ричард Фейнман заявил[38]:
Теория, согласно которой пространство непрерывно, мне кажется неверной, потому что [в квантовой механике] она приводит к бесконечно большим величинам и другим трудностям. Кроме того, она не дает ответа на вопрос о том, чем определяются размеры всех частиц. Я сильно подозреваю, что простые представления геометрии, распространенные на очень маленькие участки пространства, неверны.
Дискретное пространство-время активно обсуждалось физиками ещё в 1950-е годы в частности, в связи с проектами единой теории поля[39], однако существенного продвижения по этому пути добиться не удалось.
С. А. Векшенов считает, что для решения парадоксов необходимо ввести числовую структуру, более соответствующую интуитивно-физическим представлениям, чем канторовский точечный континуум[40]. Пример неконтинуальной теории движения предложил Садэо Сирайси[41]."
Те стрела никуда не летит -а время стоит на месте..
вопрос о стреле - это вопрос о дискретности пространства и времени
вопрос этот не решен до конца
в школе может казаться что переход к бесконечно малым величинам и пределам все решает,
но это не так
Вопрос состоит вот в чем: стрела движется непрерывно ("проходя через каждую точку") или дискретно ("прыгая" из одной точки в другую на определенном расстоянии от первой)?
до сих пор ответа нет на этот вопрос (скорее всего, нужно отказаться от канторовского точечного континуума, но как - пока нет хороших идей)
подробнее можно почитать тут: https://ru.wikipedia.org/wiki/Апории_Зенона#Современная_трактовкаhttps://ru.wikipedia.org/wiki/Апории_Зенона#Современная_трактовка
"Серьёзные исследования апорий Зенона рассматривают физическую и математическую модели совместно. Р. Курант и Г. Роббинс полагают, что для разрешения парадоксов необходимо существенно углубить наше понимание физического движения[33]. С течением времени движущееся тело последовательно проходит все точки своей траектории, однако если для любого ненулевого интервала пространства и времени нетрудно указать следующий за ним интервал, то для точки (или момента) невозможно указать следующую за ней точку, и это нарушает последовательность. Остаётся неизбежное расхождение между интуитивной идеей и точным математическим языком, предназначенным для того, чтобы описывать её основные линии в научных, логических терминах. Парадоксы Зенона ярко обнаруживают это несоответствие.
Гильберт и Бернайс высказывают мнение, что суть парадоксов состоит в неадекватности непрерывной, бесконечно делимой математической модели, с одной стороны, и физически дискретной материи, с другой[34]: мы вовсе не обязательно должны верить в то, что математическое пространственно-временное представление движения имеет физическое значение для произвольно малых интервалов пространства и времени . Другими словами, парадоксы возникают из-за некорректного применения к реальности идеализированных понятий точка пространства и момент времени , которые не имеют в реальности никаких аналогов, потому что любой физический объект имеет ненулевые размеры, ненулевую длительность и не может быть делим бесконечно.
Близкие точки зрения можно найти у Анри Бергсона и у Николя Бурбаки. Согласно Анри Бергсону[35]:
Противоречия, на которые указывает школа элеатов, касаются не столько самого движения как такового, сколько того искусственного преобразования движения, которое совершает наш разум.
Замечание Бурбаки означает, что необходимо объяснить: каким образом физический процесс за конечное время принимает бесконечно много различных состояний. Одно из возможных объяснений: пространство-время в действительности является дискретным, то есть существуют минимальные порции (кванты) как пространства, так и времени[37]. Если это так, то все парадоксы бесконечности в апориях исчезают. Ричард Фейнман заявил[38]:
Теория, согласно которой пространство непрерывно, мне кажется неверной, потому что [в квантовой механике] она приводит к бесконечно большим величинам и другим трудностям. Кроме того, она не дает ответа на вопрос о том, чем определяются размеры всех частиц. Я сильно подозреваю, что простые представления геометрии, распространенные на очень маленькие участки пространства, неверны.
Дискретное пространство-время активно обсуждалось физиками ещё в 1950-е годы в частности, в связи с проектами единой теории поля[39], однако существенного продвижения по этому пути добиться не удалось.
С. А. Векшенов считает, что для решения парадоксов необходимо ввести числовую структуру, более соответствующую интуитивно-физическим представлениям, чем канторовский точечный континуум[40]. Пример неконтинуальной теории движения предложил Садэо Сирайси[41]."
ts, прочитал труды древнегреческих авторов? или так, пост перепостить?
остальное - парадоксы
два парадокса являются частными случаями парадокса Кантора (о множествах)
Человек не может признать сам себя сумасшедшим и мотивировать этим какую-либо просьбу. Стало быть тот, кто написал закон об освобождении, сам был немного не в себе.
А описание парадокса пьяницы напомнило вот это: